Circles and Boxes and Comparing Gospels
Following on two previous posts looking at the efficacy of rectangular shapes in Venn diagrams for displaying synoptic overlap, I'd like to offer a bit more discussion of the options. For consistency, I'll continue to use the pericope divisions in the Aland Synopsis (as long as we all agree that we could and should do better).
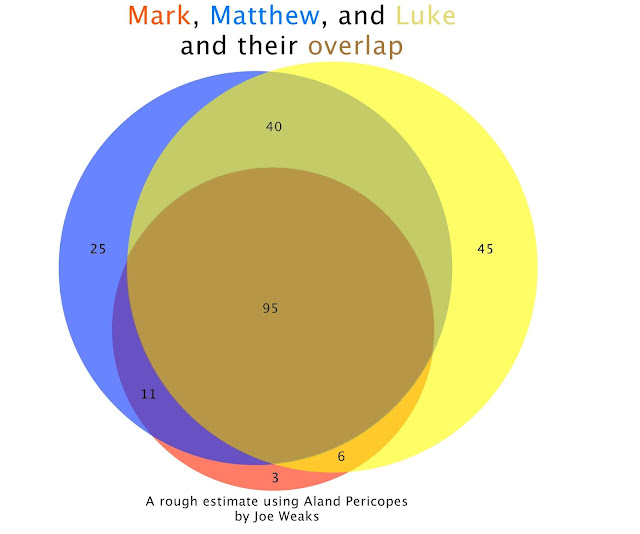
I looked first at side by side two-corpus diagrams and then at a 3-way combination diagram. I'd like to reflect on the difference between the two, as well as one more look at circles and rectangles. The data I displayed in a rectangular diagram in that last post can also easily be displayed in a more typical circular Venn diagram:
Again, circle diagrams are fantastic for today's ASMR sensibilities. But other than the aesthetic, I can't think of a single advantage of circular diagrams over rectangular Venn diagrams for two- and three-way comparisons. Look at the same data, displayed both ways, side by side. The Matthew blue circle and the Matthew blue square have the same area. Same goes for Luke and Mark, and each overlap section.
Both are able to display the data very well. To my eye, the circles are more pleasant to look at. However, the rectangles are more illustrative, in particular in ascertaining proportional relationships to the groups. In the circle diagram, I'm confused for instance in the area difference between the red uniquely Markan section and the orange Mark-Luke overlap. In the circle diagram, how do the slices for Mark-Matthew and Mark-Luke compare to each other. It's easy to see this in the rectangular diagram.
In the circle diagram, I have a hard time guessing the proportional relationships among the blue, green and yellow (uniquely Matthew, Matthew-Luke, and uniquely Luke) sections. It is much more apparent in the rectangular diagram. For pedagogy and research, I would always choose the rectangular Venn diagram.
But is the three way comparison always the ideal? Is it everything you need? Maybe not.
Here is the data in three separate two-way Venn diagrams:
If you are not focusing on the triple tradition shared component, three discreet diagrams give information you can't see in the combined graphic. Of course, it gives you, for instance, the whole amount of Mark (red) not in Luke (yellow), without regard to whether it is in Matthew. In other words, these red sections are larger than in the combined three-way diagram.
Also nice is that this configuration allows you to line up each pair so that their relative lengths stand out better. The main point is that it is illustrative, even necessary to look at both styles. They each display information not available in the other.
It is easy to say, "Well, I just need the one, because the combined three-way diagram contains all the info that was contained in the three separate ones." But because you must make decisions on how to display the diagram (what edges align, which shape/proportion to make a given area), this is far from the case. I may, in one final blog post, explore the "prolegomena"—the assumptions/decisions—when making such a diagram.





6 comments:
Hi Joe,
This is really great--very helpful. I agree that comparing the areas of arc portions of circles is not ideal. I think you're right about the advantages of squares. I would like to try a square diagram using Honoré's data on common words.
Thanks, Ms./Mr. Unknown, (ha)
I set up my formulas such that I can plug in any Mt // Lk // Mk // MtLk // MtMk // LkMk // MtLkMk data points so I can quickly produce a diagram using any data set. I think I may get a hold of 3 or 4 different sets of data and compare.
Hi Joe,
Sorry, the above comment was mine. I thought my name would show. This is Brent Nongbri. It sounds like you are way better at working with Venn Diagrams than I am. I was trying to use online tools to work with Honoré's numbers, which are slightly tricky, because he counts individual words. So, for instance, there are three different numbers for triple tradition: Matthew=8336, Mark=8630, and Luke=7884.
You will always get different numbers, depending on which gospel you use as your primary. The same is true for these experiments using Aland sections. There are many places where a section is two sections in Matthew, but the whole thing is one section in Luke, for example. The section count I've been using is different from the one Goodacre was using, as well as Larsen. Theirs was Matthew-centric. Mine is Mark, then Luke centric.
Thanks, Joe. I don't think that's right, is it, for the Larsen counts (and to be clear, I was using his method so that I could compare like with like, not because of a preference for Aland pericope counts)? There are 107 parallel Aland pericopae in Matthew and Mark -- that doesn't change depending on whether it's "Matthew-centric" or not. The thing that changes is how that is expressed as a percentage of the whole (i.e. for Mark it is 107/115 = 93%, and for Matthew it is 107/178 = 60%). The same is true for my counts for Matthew // Luke and Mark // Luke.
The reason for the different numbers in Honoré is that he is counting words within parallel Huck pericopae, not the pericopae themselves. That's where his numbers are a touch more accurate because they factor in length of parallel and non-parallel pericopae. But it's only a touch more accurate because a lot of it comes out in the wash: Matthew is much shorter than Mark in Jairus's Daughter but much longer in the Temptation, to take two striking examples.
Mark, thanks for that. To give a full treatment of my inadequacies, I published another blog post touching on the flaws in my method. https://macbiblioblog.blogspot.com/2019/05/inconsistencies-in-counting-overlapping.html
Post a Comment